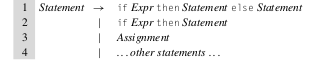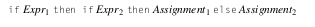En el encuentro anterior habíamos visto sobre los primeros pasos del proceso de compilación, vimos el proceso de tokenización y parseo. También vimos los problemas que aparecieron en cuanto a recursividad en el ejercicio de parser combinators. En este encuentro hablamos un poco de la teoría en cuanto a las gramáticas, los tipos de gramáticas y como resolver los problemas más comunes para poder implementar un parser y a la vez resolver problemas que puedan aparecer.
Gramáticas
Volvamos a repasar un poco la definición de gramáticas. Una gramática es un conjunto de reglas sintácticas que definen a como es un programa válido para nuestro lenguaje.
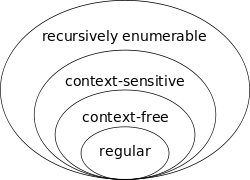
Existen distintos tipos de gramáticas, las que nos importan en nuestro ámbito son las gramáticas formales, y veremos que hay varios tipos de clasificación. Esta clasificación la hizo Noam Chomsky quien formalizó la idea de las gramáticas generativas en 1956, clasificó este tipo de gramáticas en varios tipos de complejidad creciente que forman la llamada jerarquía de Chomsky. La diferencia es que cada uno tiene reglas más particulares y restringidas, por lo que cada una genera lenguajes formales menos generales. Los más importantes y que veremos son las gramáticas libres de contexto (Tipo 2) y las regulares (Tipo 3). Estas son mucho menos generales que las gramáticas no restringidas de Tipo 0, que son solo reconocidas y que pueden procesarse mediante una máquina de turing.
Las gramáticas que veremos en este encuentro se basan en las de tipo 2 y 3, las libres de contexto y regulares. Las gramáticas regulares nos permiten describir lenguajes regulares y las mismas podemos verlas expresadas en expresiones regulares para búsqueda de patrones en un texto a buscar este patrón, lo que nos permite hacer este tipo de expresiones la búsqueda tanto de construcciones regulares finitas como infinitas
Podemos definir a cualquier gramática formalmente como una 4-tupla (Vn, Vt, P, S), donde:
- Vn es el vocabulario de noterminales; es un conjunto finito de “productores”
- Vt es el vocabulario de terminaes, caracteres del alfabeto sobre el cual se construyen las palabras del lenguaje formal que es generado por la gramática descripta; también es un conjunto finito.
- P es el conjunto finito de producciones
- S pertenece a Vn es un noterminal especial llamado axioma. Es el noterminal a partir del cual siempre deben comenzar a aplicarse las producciones que genera las palabras de un deteminado Lenguaje Formal
Cuando decimos que una gramática formal genera un lenguaje formal, significa que puede generar todas las palabras del Lenguaje Formal, pero no genera a aquellos que están fuera de las restricciones de este. De esta manera una gramática libre del contexto puede usarse para describir un lenguaje regular aunque una gramática regular no puede usarse para describir un lenguaje libre de contexto ya que la gramática regular posee mayores restricciones.
Definiciones y alcances formales de gramáticas regulares y libres de contexto.
Una gramática regular derecha es aquella cuyas reglas de producción P son de la siguiente forma:
A → a, donde A es un símbolo no-terminal en N y a uno terminal en Σ A → aB, donde A y B pertenecen a N y a pertenece a Σ A → ε, donde A pertenece a N.
Análogamente, en una gramática regular izquierda, las reglas son de la siguiente forma:
A → a, donde A es un símbolo no-terminal en N y a uno terminal en Σ A → Ba, donde A y B pertenecen a N y a pertenece a Σ A → ε, donde A pertenece a N.
Una definición equivalente evita la regla 1 (A → a) ya que es sustituible por:
A → aL
L → ε
en el caso de las gramáticas regulares derechas y por:
A → La
L → ε
en el caso de las izquierdas.
Algunos autores alternativamente no permiten el uso de la regla 3 suponiendo que la cadena vacía no pertenece al lenguaje. Un ejemplo de una gramática regular G con N = {S, A}, Σ = {a, b, c}, P se define mediante las siguientes reglas:
S → aS
S → bA
A → ε
A → cA
donde S es el símbolo inicial. Esta gramática describe el mismo lenguaje expresado mediante la expresión regular abc. Dada una gramática regular izquierda es posible convertirla, mediante un algoritmo en una derecha y viceversa. Estas gramáticas estan ya implementadas en herramientas y librerías que proveen de algo llamado expresiones regulares, y lo que permite es detectar tokens de un lenguaje regular para que podamos luego tratarlo por nuestra cuenta.
Por ejemplo de esta manera una gramática como:
S → aS es regular mientras una gramática como S → aSb no lo es.
Bien y las gramáticas libres de contexto?
Gramáticas libres de contexto
Las gramáticas libres de contexto son aquellas que tienen una construcción del tipo V → w en donde V es un no terminal y w es un conjunto de terminales y/o no terminales. El término libre de contexto se refiere al hecho de que el no terminal V puede siempre ser sustituido por w sin tener en cuenta el contexto en el que ocurra. Las gramáticas libres de contexto generan lenguajes libres de contexto y la manera de comprenderlos es mediante parsers… veremos teóricamente antes de la práctica por parsers LL. Pero antes la definición formal para aquel que le interese
Una gramática libre de contexto se la define como: 
es un conjunto finito de terminales
es un conjunto finito de no terminales
es un conjunto finito de producciones
el denominado Símbolo Inicial
- los elementos de
son de la forma
Mediante estas gramáticas los analizadores sintácticos arman derivaciones que generan justamente estructuras intermedias siendo la más inmediata y simple, los AST.
Derivaciones
Imaginemos el caso en el que tenemos una gramática como la siguiente
W → a | aS
S → ε | bS | cS
Esta describe un lenguaje del tipo a(bc)* y veamos como podría ser la transición de una entrada como abbcb:
W → aS → abS → abbS → abbcS → abbcbS → abbcb
cada uno de estos pasaje se lo denomina derivaciones y son los pasos que se realizan de acuerdo a las reglas de la gramática que generan nuestros tokens de acuerdo a la entrada.
En este caso que mostramos muestra una derivación a izquierda aunque podríamos tener también derivación a derecha. Repasemos estos conceptos
- Derivación a izquierda: en cada paso de la derivación se reemplaza el noterminal que se encuentra primero, de izquierda a derecha, en la cadena de derivación.
- Derivación a derecha: en cada paso de la derivación se reemplaza el noterminal que se encuentra primero, de derecha a izquierda, en la cadena de derivación.
Recursividad en gramáticas
Veamos un caso clásico que sucede a veces al crear una gramática para un lenguaje:
expr → expr + term | term
Veamos que si empezamos a realizar una derivación sobre esta regla gramatical:
expr → expr + term → expr + term + term → expr + term + term, la gramática en ese caso se dice que tiene una recursividad hacia izquierda si se elije su primera regla y en el caso que tengamos una implementación de un top-down parser como se explico en el encuentro anterior, estaremos ante un evento que loopeará indefinidamente. para ello se puede reformular la gramática para que pase de ser recursiva a izquierda a derecha y de esta manera que sea posible de que funcione computacionalmente con un top-down parser.
entonces teniendo una gramática genérica del tipo
X → Xα | β
la traducción mecánica a recurividad derecha es:
X → βX’
X’→ αX’ | ε
La transformación agrega un nuevo no terminal X’ en donde delega la recursividad, y para que no cicle indefinido se introduce un caso de corte con la cadena vacía.
Ahora en el caso que se tenga un ejemplo como X → Xα en donde no esta presente el otro miembro beta, imaginemos que β = ε
X → Xα |ε
pasando a recursividad por derecha
X → εX’
X’→ αX’ | ε
entonces :
X → X’
X’→ αX’ | ε
entonces queda reducido a:
X→ αX | ε
De esta manera se sigue tienendo una gramática recursiva por derecha y es el otro caso de este tipo.
Ahora veamos un caso en el que por ej:
S → Xa
X →S | aS
derivando de nuevo
S → Xa → aSa → aXaa → aSaa →aXaaa….
Se ve de nuevo que hay una recursividad por ixquierda, esto se traduce como una recursividad por izquierda indirecta, para resolver la misma basta con aplanar la gramática
S → (S | aS) a
S →Sa | aSa
se puede ver de nuevo como existe una recursividad por izquierda en el primer caso, pasamos a recursividad por derecha y se solucionará el problema:
S → aSaS’
S’ →aS’ | ε
Factorización por izquierda
Hay veces que podemos llegar a tener una gramática del siguiente tipo:
S → iEtS | iEtSeS | a
en donde el primer y segundo camino que puede tomar la derivación empiezan de la misma manera, podríamos simplificar la gramática de la siguiente manera:
S → iEtsB | a
B → ε | eS
De esta manera queda más facil la gramática y puede reemplazarse ese nuevo terminal en otros lugares que se repita la construcción. A esto se lo conoce como factorización por izquierda.
Gramáticas ambiguas
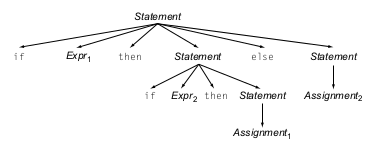
Si bien no se menciono en clase, existen gramáticas que son ambiguas y cual sería este caso? En este caso si tenemos una gramática que nos permite modelar una estructura clásica como if/else de este estilo:
Vemos que nuestro if puede ser un if Expr then Stmt siempre y el bloque else sería opcional. Ahora imaginemos que tenemos un caso en el que tenemos un if anidado en el bloque then de otro if:
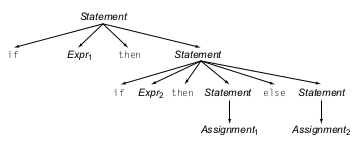
En este caso nuestro parser no sabrá a que contexto pertenece nuestro bloque else cuando lo parseemos con un top-down parser, y se podrían generar dos resultados distintos de AST, uno en el que el bloque else pertenece al segundo if anidado, que sería nuestro escenario deseado:
Y otro resultado en el que el bloque else pertenece al primer if
En este caso se dice que la gramática es ambigua ya que una vez armado uno de los dos AST no sabremos si el resultado que generamos era el deseado o no.
Para eliminar la ambigüedad en este ejemplo, basta con reescribir nuestra gramática de una manera que podamos distinguir cuando tenemos una gramática del tipo if/then o if/then/else. Entonces nuestra gramática podría quedar como:
Autómatas
Si bien no lo mencionamos en el encuentro anterior, tenemos una manera de reconocer a los lenguajes regulares, y es mediante una máquina que nos permite a partir de una entrada ir cambiando de estado hasta llegar a un estado final correcto, y si no llega a ninguna salida una vez terminada la entrada entonces nuestra entrada es inválida para esa máquina en particular. A esta máquina se la conoce como autómata finito. Formalmente, un autómata finito es una 5-tupla (Q, Σ, q0, δ, F) donde:
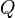es un conjunto finito de estados;
es un alfabeto finito;
es el estado inicial;
es una función de transición;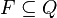
es un conjunto de estados finales o de aceptación.
Representación como diagramas de estados
Los estados Q se representan como vértices, etiquetados con su nombre en el interior.Los autómatas finitos se pueden representar mediante grafos particulares, también llamados diagramas de estados finitos, de la siguiente manera: Una transición δ desde un estado a otro, dependiente de un símbolo del alfabeto, se representa mediante una arista dirigida que une a estos vértices, y que está etiquetada con dicho símbolo. El estado inicial q0 se caracteriza por tener una arista que llega a él, proveniente de ningún otro vértice. El o los estados finales F se representan mediante vértices que están encerrados a su vez por otra circunferencia
Un autómata finito determinista (abreviado AFD) es un autómata finito que además es un sistema determinista; es decir, para cada estado q ∈ Q en que se encuentre el autómata, y con cualquier símbolo a ∈ Σ del alfabeto leído, existe siempre a lo más una transición posible δ(q,a).
- En un AFD no pueden darse ninguno de estos dos casos:Que existan dos transiciones del tipo δ(q,a)=q1 y δ(q,a)=q2, siendo q1 ≠ q2;
- Que existan transiciones del tipo δ(q, ε), salvo que q sea un estado final, sin transiciones hacia otros estados.
Un ejemplo interesante de autómatas finitos deterministas son los tries.
Un autómata finito no determinista (abreviado AFND) es aquel que, a diferencia de los autómatas finitos deterministas, posee al menos un estado q ∈ Q, tal que para un símbolo a ∈ Σ del alfabeto, existe más de una transición δ(q,a) posible.
Haciendo la analogía con los AFDs, en un AFND puede darse cualquiera de estos dos casos:
- Que existan transiciones del tipo δ(q,a)=q1 y δ(q,a)=q2, siendo q1 ≠ q2;
- Que existan transiciones del tipo δ(q, ε), siendo q un estado no-final, o bien un estado final pero con transiciones hacia otros estados.
Cuando se cumple el segundo caso, se dice que el autómata es un autómata finito no determinista con transiciones vacías o transiciones ε (abreviado AFND-ε). Estas transiciones permiten al autómata cambiar de estado sin procesar ningún símbolo de entrada.
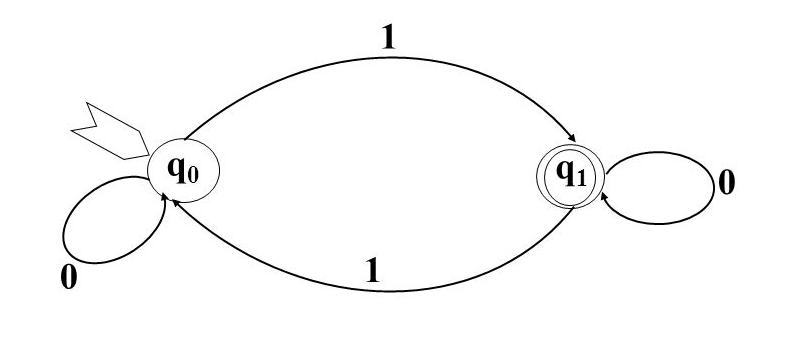
Ahora un ejemplo de un AFD sería un caso en el que querramos tener un lenguaje que reconozca un número impar de 1’s
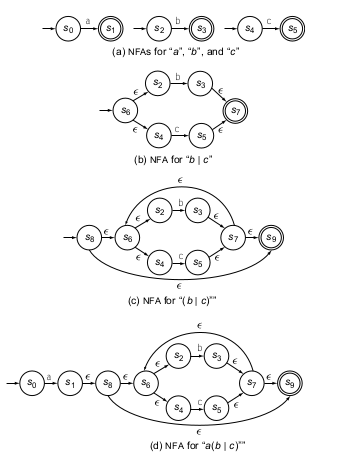
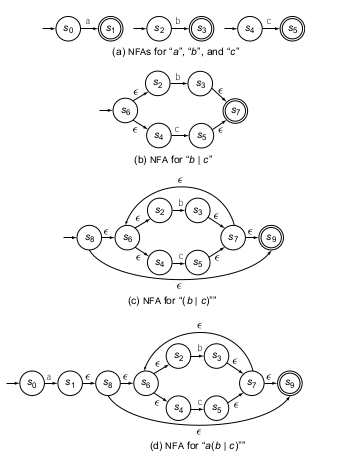
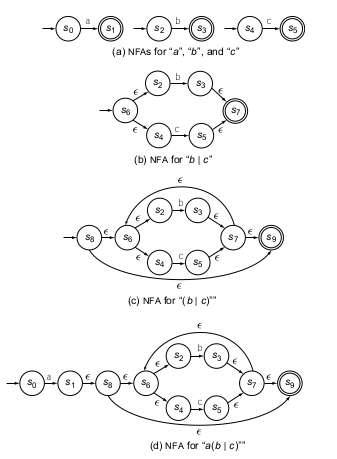
Ahora veamos otro caso en el que se quiere armar un AFND que permita reconocer una regex del tipo a(b|c)*. Primero armemos tres AFD que reconozca a, b y c solamente y por separado, esto se puede ver en (a) de la siguiente imagen.
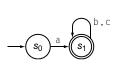
Ahora por parte veamos como puede ser armando la parte de adentro del operador *, o sea b|c , el diagrama se puede ver en (b). Ahora agreguemos el operador * a esta gramática anterior, esto se ve en (c). Ahora solo falta agregar un a antes de este AFND, esto se ve en (d). Ahora vemos que nuestro AFND-ε es bastante complejo, empecemos a eliminar las transiciones ε que no nos suman en realidad a un cambio de estado y veremos que b y c nos generan un estado final uno o mas, y que estos puede ciclar indefinidamente, y puede haber 0 o más iteraciones de una de estas dos opciones, entonces una entrada a ya pasa de un estado inicial a uno final, por lo que se asemeja al AFD de a en el diagrama en (a). Ahora si queremos que haya n entradas siendo n>= 0 y sea b|c entonces agreguemos al estado final un bucle que reconozca tanto b o c. Esto genera el siguiente AFND.
Aqui se ve una manera de pasar de AFND-ε a AFND y se simplificó el autómata.
Simplificación de gramáticas
Se explico sobre la simplificación de una gramática por medio de reemplazo de no terminales en otros no terminales y de ahi eliminar primero recursividad por izquierda y luego factorizar de alguna manera la gramática.
Ejercicios
-
Dada las siguientes gramáticas defina si hay recursividad por izquierda, si se puede factorizar, luego si la gramática es regular y simplificar la misma si se puede.
S → SS* | SS+ | a
A→Cd
B→Ce
C → A| B | f -
Armar un parser combinator en scala para una entrada que pertenece a un código de un lenguaje acotado en la que se pueden definir comentarios, clases y métodos, dentro de los métodos solo se puede mostrar un número o string o realizar una expresión matemática, del estilo 2+3 o 4-2 pero simple sin encadenamiento con otras operaciones.